3. 머신러닝(지도학습-회귀)
1. 회귀 개념
회귀 분석: 데이터를 가장 잘 설명하는 모델을 찾아 입력값에 따른 미래 결과값을 예측하는 알고리즘이다.
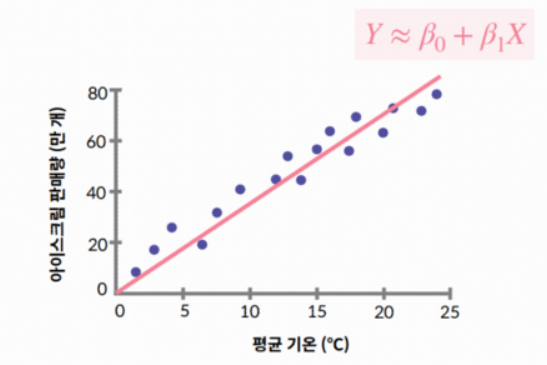
당신이 아이스크림 가게를 운영하는 주인이라고 가정해보자.
판매용 아이스크림 주문 시, 예상되는 실제 판매량만큼만 주문을 원한다.
이때 만약 평균 기온을 활용하여 미래 판매량을 예측할 수 있다면?
문제정의
- 데이터: 과거 평균 기온(X)과 그에 따른 아이스크림 판매량(Y)
- 가정: 평균 기온과 판매량은 선형적인 관계를 가지고 있다.
- 목표: 평균 기온에 따른 아이스크림 판매량 예측하기
| 평균기온(X) | 아이스크림 판매량(Y) |
| 10 | 40 |
| 13 | 52.3 |
| 20 | 60.5 |
| 25 | 80 |
주어진 데이터
X: 평균 기온
Y: 아이스크림 판매량
가정
𝑌 ≈ 𝛽0 + 𝛽1 -> 적절한 𝛽0 𝛽1 값을 찾자! (Y = ax + b)
완벽한 예측은 불가능하기에 최대한 잘 근사해야 한다!
각 데이터의 실제 값과 모델이 예측하는 값의 차이를 최소한으로 하는 선을 찾자!
2. 단순 선형 회귀
단순 선형 회귀란?
-> 데이터를 설명하는 모델을 직선 형태로 가정
가정
𝑌 ≈ 𝛽0 + 𝛽1
직선을 구성하는 𝛽0 (y절편)와 𝛽1 (기울기)를 구해야함
데이터를 잘 설명한다는 것은 어떤것일까?
실제 정답과 내가 예측한 값과의 차이가 작을수록 좋지 않을까?

실제 값과 예측 값의 차이를 구해보자
| 입력값 | 예측값 | 실제값 | 실제값 - 예측값 | (실제값 - 예측값)^2 |
| 2 | 2 | 3 | 1 | 1 |
| 4 | 4 | 5 | 1 | 1 |
| 6 | 6 | 3 | -3 | 9 |
| 8 | 8 | 7 | -1 | 1 |
| 합계 | -2 | 12 |

단순 선형 회귀 특징
- 가장 기초적이나 여전히 많이 사용되는 알고리즘
- 입력값이 1개인 경우에만 적용이 가능
- 입력값과 결과값의 관계를 알아보는데 용이함
- 입력값이 결과값에 얼마나 영향을 미치는지 알 수 있음
- 두 변수 간의 관계를 직관적으로 해석하고자 하는 경우 활용
실습하기
단순 선형 회귀 분석하기 - 데이터 전 처리
기계학습 라이브러리 scikit-learn을 사용하면 Loss 함수를 최솟값으로 만드는 β0, 을 쉽게 구할 수 있습니다.
주어진 데이터를 sklearn에서 불러 올 선형 모델에 적용하기 위해서는 전 처리가 필요합니다.
이번 실습에서는 sklearn에서 제공하는 LinearRegression을 사용하기 위한 데이터 전 처리를 수행해보겠습니다.
sklearn의 LinearRegression 입력 값 형태
LinearRegression 모델의 입력값으로는 Pandas의 DataFrame의 feature (X) 데이터와 Series 형태의 label (Y) 데이터를 입력 받을 수 있습니다.
X, Y의 샘플의 개수는 같아야 합니다.
import pandas as pd
from sklearn.linear_model import LinearRegression
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
"""
1. X의 형태를 변환하여 train_X에 저장합니다.
"""
train_X = pd.DataFrame(X, columns=['X']) # X를 column 명이 'X'인 Dataframe으로 변환합니다.
"""
2. Y의 형태를 변환하여 train_Y에 저장합니다.
"""
train_Y = pd.Series(Y) # Y를 Series로 변환합니다.
# 변환된 데이터를 출력합니다.
print('전 처리한 X 데이터: \n {}'.format(train_X))
print('전 처리한 X 데이터 shape: {}\n'.format(train_X.shape))
print('전 처리한 Y 데이터: \n {}'.format(train_Y))
print('전 처리한 Y 데이터 shape: {}'.format(train_Y.shape))실행 결과

단순 선형 회귀 분석하기 - 학습하기
기계학습 라이브러리 scikit-learn을 사용하면 Loss 함수를 최소값으로 만드는 β0, 을 쉽게 구할 수 있습니다.
[실습1]에서 전 처리한 데이터를 LinearRegression 모델에 입력하여 학습을 수행해봅시다.
LinearRegression (sklearn)
LinearRegression을 사용하기 위해서는 우선 해당 모델 객체를 불러와 초기화해야 합니다.
아래 코드는 lrmodel에 모델 객체를 초기화 하는 것을 보여줍니다.
lrmodel = LinearRegression()
모델 초기화를 수행했다면 전 처리된 데이터를 사용하여 학습을 수행할 수 있습니다.
아래코드와 같이 fit 함수에 학습에 필요한 데이터를 입력하여 학습을 수행합니다.
lrmodel.fit(train_X, train_Y)
LinearRegression의 β, β1값을 구하기 위해서는 아래 코드를 사용하여 구할 수 있습니다.
beta_0 = lrmodel.intercept_ beta_1 = lrmodel.coef_[0]
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
import elice_utils
eu = elice_utils.EliceUtils()
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
train_X = pd.DataFrame(X, columns=['X'])
train_Y = pd.Series(Y)
"""
1. 모델을 초기화 합니다.
"""
lrmodel = LinearRegression()# LinearRegression 모델을 초기화 합니다.
"""
2. train_X, train_Y 데이터를 학습합니다.
"""
lrmodel.fit(train_X, train_Y) # train_X와 train_Y를 이용하여 모델을 학습 시킵니다.
# 학습한 결과를 시각화하는 코드입니다.
plt.scatter(X, Y)
plt.plot([0, 10], [lrmodel.intercept_, 10 * lrmodel.coef_[0] + lrmodel.intercept_], c='r')
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.title('Training Result')
plt.savefig("test.png")
eu.send_image("test.png")
실행 결과

단순 선형 회귀 분석하기 - 예측하기
기계학습 라이브러리 scikit-learn 을 사용하면 Loss 함수를 최소값으로 만드는 β0\beta_0, β1\beta_1 을 쉽게 구할 수 있습니다.
위의 학습한 모델을 바탕으로 예측 값을 구해봅시다.
LinearRegression (sklearn)
LinearRegression을 사용하여 예측을 해야한다면 아래와 같이 predict 함수를 사용합니다.
pred_X = lrmodel.predict(X)
predict 함수는 DataFrame 또는 numpy array인 X 데이터에 대한 예측값을 리스트로 출력합니다.
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
train_X = pd.DataFrame(X, columns=['X'])
train_Y = pd.Series(Y)
# 모델을 트레이닝합니다.
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
"""
1. train_X에 대해서 예측합니다.
"""
pred_X = lrmodel.predict(train_X) # predict() 를 이용하여 예측합니다.
print('train_X에 대한 예측값 : \n{}\n'.format(pred_X))
print('실제값 : \n{}'.format(train_Y))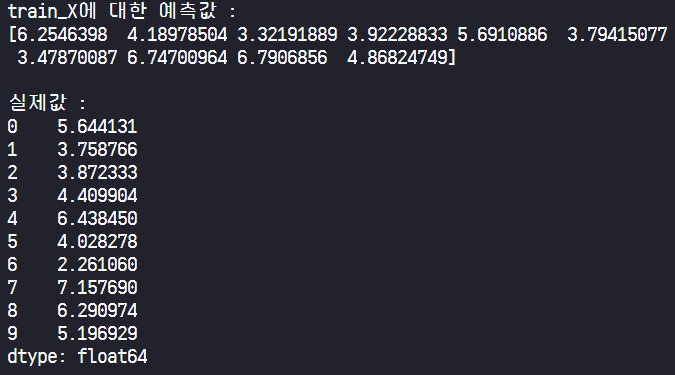
3. 다중 선형 회귀
만약, 입력값 X에 강수량이 추가된다면?
즉, 평균 기온(X1)과 평균 강수량(X2)에 따른 아이스크림 판매량(Y)을 예측하고자 함
여러 개의 입력값으로 결과값을 예측하고자 하는 경우 -> 다중 선형 회귀(Multiple Linear Regresstion)
다준 선형 회귀 모델 이해하기
입력값 X가 여러개(2개 이상)인 경우 활용할 수 있는 회귀 알고리즘
각 개별 Xi에 해당하는 최적의 𝛽i를 찾아야함
-> 𝑌 ≈ 𝛽0 + 𝛽1𝑋1 + 𝛽2𝑋2 + 𝛽3𝑋3 + ⋯+ +𝛽m 𝑋m
평균 기온(X1)과 평균 강수량(X2)에 따른 아이스크림 판매량(Y)을 예측
-> 𝑌 ≈ 𝛽0 + 𝛽1𝑋1 + 𝛽2𝑋2
다중 선형 회귀 특징
- 여러 개의 입력값과 결과값 간의 관계 확인 가능
- 어떤 입력값이 결과값에 영향을 미치는지 알 수 있다.
- 여러 개의 입력값 사이의 상관관계가 높을 경우 결과에 대한 신뢰성을 잃을 가능성이 있음
실습하기
다중 회귀 분석하기 - 데이터 전 처리
다중 회귀 분석(Multiple Linear Regression)은 데이터의 여러 변수(features) XX를 이용해 결과 YY를 예측하는 모델입니다.
마케터들에게는 광고 비용에 따른 수익률을 머신러닝을 통해서 예측할 수 있다면 어떤 광고 플랫폼이 중요한 요소인지 판별할 수 있을 것입니다.
아래와 같이 FB, TV, Newspaper 광고에 대한 비용 대비 Sales 데이터가 주어졌을 때, 이를 다중 회귀 분석으로 분석해봅시다.

우선 데이터를 전 처리 하기 위해서 3개의 변수를 갖는 feature 데이터와 Sales 변수를 label 데이터로 분리하고
학습용, 평가용 데이터로 나눠봅시다.
import pandas as pd
from sklearn.model_selection import train_test_split
df = pd.read_csv("data/Advertising.csv")
print('원본 데이터 샘플 :')
print(df.head(),'\n')
# 입력 변수로 사용하지 않는 Unnamed: 0 변수 데이터를 삭제합니다
df = df.drop(columns=['Unnamed: 0'])
"""
1. Sales 변수는 label 데이터로 Y에 저장하고 나머진 X에 저장합니다.
"""
X = df.drop(columns=['Sales'])
Y = df['Sales']
"""
2. 2:8 비율로 (test_size = 0.2) X와 Y를 학습용과 평가용 데이터로 분리합니다.
"""
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
# 전 처리한 데이터를 출력합니다
print('train_X : ')
print(train_X.head(),'\n')
print('train_Y : ')
print(train_Y.head(),'\n')
print('test_X : ')
print(test_X.head(),'\n')
print('test_Y : ')
print(test_Y.head())

다중 회귀 분석하기 - 학습하기
위에서 전 처리한 데이터를 바탕으로 다중 선형 회귀 모델을 적용해보겠습니다.
다중 선형 회귀 또한 선형 회귀 모델과 같은 방식으로 LinearRegression을 사용할 수 있습니다.
이번 실습에서는 학습용 데이터를 다중 선형 회귀 모델을 사용하여 학습하고, 학습된 파라미터를 출력해봅시다.
LinearRegression (sklearn)
LinearRegression의 beta와 같은 파라미터들은 아래 코드와 같이 구할 수 있습니다.
lrmodel = LinearRegression() lrmodel.intercept_ lrmodel.coef_[i]
intercept_는 β0에 해당하는 값이고, coef_[i]는 i+1 번째 변수에 곱해지는 파라미터 값을 의미합니다.
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
"""
1. 다중 선형 회귀 모델을 초기화 하고 학습합니다
"""
lrmodel = LinearRegression() # LinearRegression 모델을 초기화 합니다.
lrmodel.fit(train_X, train_Y) # train_X와 train_Y 데이터로 모델을 학습합니다.
"""
2. 학습된 파라미터 값을 불러옵니다
"""
beta_0 = lrmodel.intercept_ # y절편 (기본 판매량)
beta_1 = lrmodel.coef_[0] # 1번째 변수에 대한 계수 (페이스북)
beta_2 = lrmodel.coef_[1] # 2번째 변수에 대한 계수 (TV)
beta_3 = lrmodel.coef_[2] # 3번째 변수에 대한 계수 (신문)
print("beta_0: %f" % beta_0)
print("beta_1: %f" % beta_1)
print("beta_2: %f" % beta_2)
print("beta_3: %f" % beta_3)실행 결과

다중 회귀 분석하기 - 예측하기
위에서 학습한 다중 선형 회귀 모델을 바탕으로 이번엔 새로운 광고 비용에 따른 Sales 값을 예측해봅시다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
# 다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
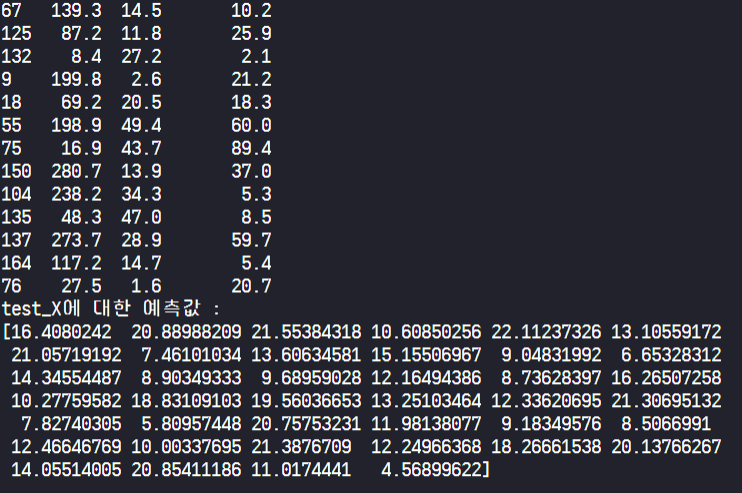
print('test_X : ')
print(test_X)
"""
1. test_X에 대해서 예측합니다.
"""
pred_X = lrmodel.predict(test_X) # predict()를 활용해서 예측합니다.
print('test_X에 대한 예측값 : \n{}\n'.format(pred_X))
# 새로운 데이터 df1을 정의합니다
df1 = pd.DataFrame(np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1]]), columns=['FB', 'TV', 'Newspaper'])
print('df1 : ')
print(df1)
"""
2. df1에 대해서 예측합니다.
"""
pred_df1 = lrmodel.predict(df1) # predict()를 활용해서 예측합니다.
print('df1에 대한 예측값 : \n{}'.format(pred_df1))실행 결과